Research on Single-antenna FMCW Radar Launch Leakage Signal Suppression Technology

Abstract single antenna FMCW radar transmit signal leakage, taking into account the strength of the adaptive control system, data processing capability, accurate and flexible, etc., an adaptive cancellation aspect, and the simulation and experiment results show that The scheme effectively suppresses the problem of the transmission leakage signal caused by insufficient transmission and reception isolation.

This article refers to the address: http://

Due to limitations in size, weight, cost, etc., most of the continuous wave system radar seekers use a single antenna technology. Due to insufficient transmission and reception isolation, the transmitted signal leaks into the receiver to generate a leakage signal, and the signal leakage causes continuous wave system radar reception. The sensitivity of the machine drops, and the mid-range, microwave mixer or pre-low noise amplifier is saturated.

With the development of components, the saturation power of millimeter-wave front-end devices, such as mixers, can reach more than a dozen dBm. In the missile-borne environment, the power of continuous wave transmitters is generally several hundred mW. Therefore, saturation is not the main The problem is only to focus on solving the problem of reduced receiver sensitivity. At the same time, considering the uncertainty of the actual information process, this paper uses adaptive numbers.

The word cancellation technology comprehensively processes the information process and minimizes the emission leakage signal due to insufficient transceiver isolation.

1 The basic principle of adaptive digital cancellation

The working principle of the adaptive digital cancellation system is shown in Figure 1.

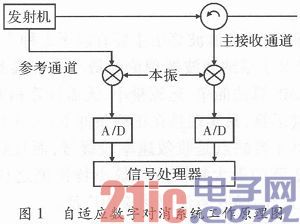
In this model, the receiver has two independent channels, the reference receive channel and the primary receive channel. The reference channel samples the transmitted signal, and the primary receive channel includes a transmit leakage signal and a target echo signal. The main echo signal and the reference signal are respectively sent to the intermediate frequency adaptive digital canceller, and the amplitude and phase of the signals received by the two channels are different. To extract the useful target reflected signal, only the received reference signal needs to be adjusted, so that the reference signal is received. It is consistent with the emission leakage signal in the main signal, so that a good cancellation effect is obtained.

The adaptive filter is different from the ordinary filter. Its impulse response or filtering parameters change with the change of the external environment. After an automatically adjusted convergence time, the optimal filtering requirements are achieved. The block diagram of the cancellation principle is shown in Figure 2.

Let the main echo signal d(n) be the sum of the target echo signal s(n) and the emission leakage signal z(n), x(n) is the reference signal, and x(n) is not related to the target echo signal, but There is some unknown correlation with z(n), and x(n) is filtered to produce a signal z'(n) similar to z(n), and finally the output of the system is obtained.

y(n)=s(n)+z(n)-z'(n) (1)

Let z(n), x(n), and s(n) be zero-mean stationary stochastic processes. s(n) is not related to z(n). and

Y2(n)=s2(n)+(z(n)-z'(n))2+2s(n)(z(n)-z'(n)) (2)

Taking mathematical expectation on both sides of equation (2), since s(n) is not related to z(n) and x(n), s(n) is not related to z'(n), so

E[y2(n)]=E[s2(n)]+E[(z(n)-z'(n))2] (3)

The signal power E[s2(n)] is independent of the adjustment of the adaptive filter. Therefore, the adaptive filter adjustment minimizes E[y2(n)], ie E[(z(n)-z'(n)) 2] The smallest. And because z(n)-z'(n)=y(n)-s(n), the adaptive leakage signal cancellation system when E[(z(n)-z'(n))2] is the smallest The mean square error E[(y(n)-s(n))2] of the output signal y(n) and the useful signal s(n) is also the smallest. In the ideal case, z(n)=z'(n) , then y(n)=s(n).

However, in the actual system, the signal received from the antenna is more complicated than the theoretical analysis, and the cancellation is relatively low.

The adaptive filter itself has an important adaptive algorithm, which can modify the filtering parameters according to certain criteria according to the input, output and original parameter values, so that the adaptive filter can effectively track the changes of the external environment.

At present, there are three main types of adaptive filtering algorithms:

(1) Minimum mean square error (LMS) algorithm based on Wiener filter theory. The LMS algorithm is simple, the calculation amount is small, and it is not necessary to calculate the correlation function and the matrix inversion operation, which is easy to implement and can obtain satisfactory performance under the correct conditions. The main disadvantage is that the convergence rate is slow, and it is sensitive to the change of the ratio of the maximum eigenvalue to the minimum eigenvalue of the tap input correlation matrix. Even so, the LMS algorithm is still widely used.

(2) Recursive Least Squares (RLS) algorithm based on least squares method. The advantage of the RLS algorithm is that it has fast convergence speed and strong tracking ability, but its computational complexity is much larger than that of the LMS algorithm due to matrix inversion, which limits its application.

(3) Kalman algorithm based on Kalman filter theory. The Kalman algorithm has good convergence performance, strong tracking ability and robust convergence rate (Robust). It is insensitive to input dependent short-array eigenvalues; and, the algorithm is applicable to stationary stochastic processes and non-stationary stochastic processes. The main disadvantage is that the matrix representation in the Kalman filter formula is directly used, the algorithm is complex, the amount of calculation is large, and the numerical stability is poor.

This paper chooses the LMS algorithm to complete the adaptive digital cancellation.

2 Theoretical data simulation analysis

The simulation results are shown in Figures 3 and 4.

Fig. 3(a) shows the main echo signal d(n), Fig. 3(b) shows the target echo signal s(n); Fig. 3(c) shows the output signal after cancellation, it can be seen that after a period of time The adaptive adjustment can not see the emission leakage signal after the cancellation of the output signal. It can be seen that the system has a good cancellation effect on the transmission leakage signal, and the waveform distortion is small.

4 is a time domain waveform of the signal response, FIG. 4(a) is a frequency domain pattern corresponding to the main echo signal d(n); FIG. 4(b) is a frequency domain pattern corresponding to the output signal after cancellation, and comparison is known. The leakage signal is reduced by approximately 40 dB.

3 Simulation analysis of actual mining data

In the actual data, the transmit leakage signal and the reference signal are both 20 MHz sine waves, and the target echo signal is a 21 MHz sine wave with a data sampling rate of 200 MHz. The signal response time domain waveform is shown in Figure 5.

Fig. 5(a) shows the main echo signal d(n); Fig. 5(b) shows the output signal after cancellation, and it can be seen that the output after cancellation can substantially restore the target echo signal, and the waveform distortion is small.

FIG. 6 is a frequency domain diagram corresponding to the signal shown in FIG. 5. By comparison, the leakage signal is reduced by about 32.2 dB.

4 Conclusion

Based on theoretical analysis and experimental verification, this paper can reduce the emission leakage signal accurately and flexibly, and reduce the impact of leakage signal on receiver sensitivity by adopting adaptive digital cancellation technology for the signal leakage problem of 3 mm frequency modulated continuous wave radar. . Theoretical simulation and experimental test results show that the method is effective and feasible.